Mieszkanie na sprzedaż Wrocław, Lipa Piotrowska
613 930 zł
Szczegóły oferty
| Symbol oferty | BESW-MS-14264 |
| Powierzchnia | 62,71 m² |
| Powierzchnia użytkowa [m2] | 62,71 m² |
| Powierzchnia balkonów/tarasów | 4,95 m² |
| Liczba pokoi | 3 |
| Liczba sypialni | 1 |
| Rodzaj budynku | dom wielorodzinny |
| Piętro | parter |
| Liczba pięter w budynku | 2 |
| Stan lokalu | deweloperski |
| Okna | PCV |
| Balkon | jest |
| Liczba balkonów | 1 |
| Rok budowy | 2024 |
| Plac zabaw | tak |
| Umeblowanie | brak |
| Usytuowanie | trójstronne |
| Rolety antywłamaniowe | tak |

Opis nieruchomości
BEZPOŚREDNIO od dewelopera, brak prowizji oraz podatku 2% PCC.
Posiadamy ponad 90 inwestycji we Wrocławiu i okolicach, zapytaj o pozostałe.
Bezpłatna pomoc przy kredytowaniu.
Inwestycja na Północy Wrocławia, Lipa Piotrowska, mieszkania w stanie deweloperskim, planowany odbiór 31.12.2024r.
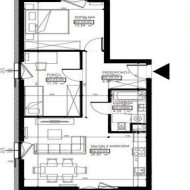
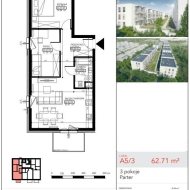
Prezentowane mieszkanie o powierzchni użytkowej 62,71 m.kw, składa się z salonu z aneksem kuchennym o pow. 25,47 m.kw, sypialni o pow. 12,54 m.kw, pokoju o pow. 11,29 m.kw, łazienki o pow. 4,33m2 oraz przedpokoju o pow. 8,58m2. Z salonu wyjście na balkon o pow. 4,95m.kw od strony południowej.
Posiadamy mieszkania od 42,20m.kw. do 72,50 m.kw. na różnych piętrach, zadzwoń i umów się na spotkanie.
Świetna lokalizacja w pobliżu znajdują się sklepy, przystanek autobusowy 100 m, 5 minut do obwodnicy S8, przedszkole, szkoła, przychodnia.
Cena: 613 930zł + miejsce w garażu podziemnym 30 000 - 45 000 zł
Cena komórki lokatorskiej wynosi 16 900 - 22 900zł.
Zadzwoń, umów się na prezentację.
Kontakt:
Renner Agnieszka
BESTATE Wrocław
tel: 602 459 354
e-mail: arenner@bestate.com.pl
Nr licencji: 22004
www.bestate.com.pl
Lokalizacja nieruchomości
Podobne oferty
DYREKTOR ODDZIAŁU